Which database when for AI: Are vector databases all you need?

Semantic search is the dream of many of us data users. What if I could just describe in plain language what data I wanted to get, and automagically the correct answer would appear. It would be the realization of Star Trek's boringly named but oh-so-amazing "computer": "Computer, search for the term 'Darmak' in all linguistic databases for this sector".

Advances in Generative AI, specifically Large Language Models, might make it seem like this dream is already reality. Are the days of guessing the right keywords to get relevant answers truly over? Can we forget data extraction pipelines feeding into structured data warehouses, and just query data directly with natural language? Can we just put our documents in a vector database, and get everything we need with natural language rather than using a programming language?

Another reason for interest in vector databases comes from the letter "R" of the popular GenAI technique RAG. RAG stands for "retrieval augmented generation", and was introduced in the 2020 paper Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks. To make available targeted, typically local knowledge to an LLM's generation capabilities, RAG implementations first retrieve relevant data context (e.g. using semantic search), and then add the retrieved data (“augment”) to the original LLM task description for generation. Reasons to use RAG rather than just G ("generate") are 1.) when needed information is not a part of the data used to train the LLM (e.g. local or obscure knowledge) and 2.) to reduce hallucinations.

In nearly all articles and blog posts I have seen about RAG, the retrieval mechanism involves semantic similarity as calculated in some vector database (aka Maximum Inner Product Search as in the original RAG paper; other examples include this NVIDIA blog post, the LlamaIndex guide to RAG, and this langchain tutorial). As we will see below, however, the world of information retrieval is much bigger and older than vector databases.

In this post and its follow-up, we flesh out the options---both old and new---for extracting data to answer business questions. What database technology you should use when for your AI product will depend of course on the problem you are trying to solve. It also depends on where you are in your AI Strategy journey: Are you still performing rapid experiments to find the value for your business ("Day 0"), or are you figuring out how to bring together multiple AI products with similar but not identical data query needs when scaling AI in Day N?

What you won’t find in this post is a broad pro-con listing of all vendors and tech choices, as what matters most is the specific fit for your business need, not generic pluses and minuses. You also won’t find a narrow “getting-started” guide to vector databases for AI, as these already exist in bulk, and---in my opinion---rarely capture key features required by business use-cases that are needed before releasing an AI product within Day 1 work.

What you will find in this post is an articulation of a business relateable data query task and where different database options shine or struggle. The example data and query tasks we use are self-contained, but are still more complex than typical quick-start guide tasks that tend to highlight the strengths of a technology while avoiding its weaknesses.

You’ll also find principles for which database to choose when, rooted in both the example tasks of this post plus broader experience and expertise.

So let’s get started! The first blog post in this two-part series introduces the example tasks we will be using to better understand the theory and practice of databases for AI. It also gives an overview of databases for AI, with special emphasis on vector databases and the main reason for the current interest in vector databases, the so-called vector embeddings of natural language.

In the second blog post, we'll see both relational and vector databases in action as we attempt to answer our example tasks. While we don't offer completely self-contained demos, we do give code snippets to convey the look and feel of working with different databases in your AI projects. We then wrap up with final reflections on the current state-of-the-art, and how this impacts decisions your business or team may be facing.

Along the way, we highlight the common mistake LGTMIANGE ("looks-good-to-me-is-almost-never-good-enough"), and will dive into German Masters Swimming results, with emphasis on how this toy data problem relates to actual business problems ("Masters" in this context just means swimming for older people).

Example tasks: Semantic and structured question answering on German masters swimming data

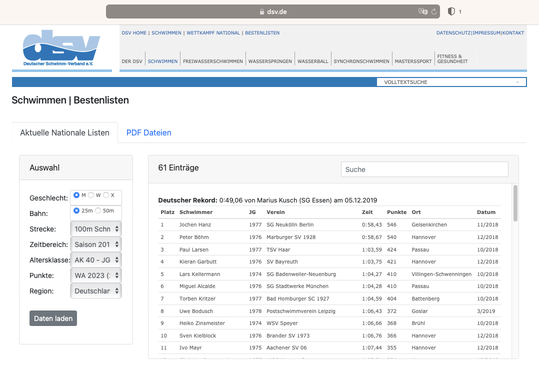
To have a common working example, let's say you share my interest in German masters swimming results for 100 meter butterfly races, and you want to automate your usual status-quo process of navigating to the website, clicking on the gender of interest ("Geschlecht"), selecting races from 25 meter or 50 meter pools, choosing 100m butterfly races ("Strecke"), choosing a time-window ("Zeitbereich"), and then choosing the age-group of interest ("Altersklasse") as in the below screenshot:

Let's say further you have access to race descriptions for each of these races via YouTube transcriptions of streamed race coverage (Note: this part is fictional for illustrative purposes. If, however, you know of an actual YouTuber with such race coverage, please let me know).

The challenge of domain-specific vocabulary for AI

Pulling back the curtain on how we created fictitious race descriptions gives a lesson in how important domain knowledge and vocabulary are for business tasks, and how challenging they can be for AI. The race descriptions were generated by an LLM that was given per race a characterization of the start, turns and swimmer technique. While investigating performance on the tasks described below, I realized that some of the mistakes arose because the LLM generating the descriptions got confused by swimming-specific terminology. For example, any swimmer knows that a "long turn" is bad, but a "long stroke (technique)" is generally good, yet one generated description included the phrase “he maintained a long turn“. This race description was incorrectly retrieved when searching for good turns. In business contexts, domain knowledge and vocabulary are often decisive in AI performance.

You also want to link the free-text race descriptions to the tabular results data from the German Masters Swimming website so you can capture qualitative facets of the races, like who had a good first turn, who had a good start, or who was so tired at the end of the race that it seemed they were carrying a piano on their back (thanks, Coach Steve, for sharing this assessment of my first 200m long course butterfly race).

The chances are good that you don't share this interest of mine, so let's spend a minute connecting the above data-querying tasks to actual business contexts, such as

• In e-commerce: searching for positive or negative customer product reviews over a definite subset of your products, such as date ranges of when the product was sold

• In insurance: searching for automobile claims descriptions restricted to specific makes of car, coverage years or customer profile

• In banking: searching during KYC ("know your customer") for similar business activity descriptions among past customers engaged in fraudulent or illicit activities.

We will consider three search tasks on this swimming dataset, with the first one playing to the strengths of vector databases (more on these below), the second one a natural for structured, relational databases, and the third requiring some mixture of the two.

Task 1 (semantic): Answer the question, "For which 100 butterfly races in the dataset race-descriptions.json did the swimmer have a good turn?"

We consider this task as an example of "semantic" search, rather than structured (e.g. SQL) search, since the question of whether or not a turn was good is not explicitly given in one of the dataset fields, but rather has to be inferred from the meaning ("semantics") of the race-description fields.

Cheat: sneaking relational-like filtering into the semantic search task

The restriction "in the dataset" is a cheat for the the relational-like condition "in Germany between 2017 and 2020 for men in the 100m butterfly for the age group 40-44", since those are the date ranges included in this dataset. In applications, it is rare that your question is equally interested across all data that you have.

Here are the first 5 swims featuring a good turn, ordered by the id column. From the race text description, we’ve pulled out the sentence describing a turn in the column turn-content.

id	schwimmer	datum	turn-content
1	Jochen Hanz	2017-11-01	However, he made up for it with a great first turn, propelling himself forward with strong underwater dolphin kicks.
2	Peter Böhm	2017-12-01	As he approached the first turn, he executed a smooth and quick flip.
4	Michael Schmitz	2017-12-01	He had a fast second turn during the 100m butterfly race.
5	Dirk Neuhaus	2017-12-01	During the second turn, he executed a fast maneuver.
8	Paul Larsen	2018-02-01	He had a great 1st turn as he approached the wall.

Task 2 (relational): Answer the question, "What were the top 10 times in Germany for the seasons 2017-2018 and 2018-2019 for men in the 100m butterfly for the age group 40-44?".

This task plays to the strengths of relational databases, as well as other structured databases like NoSQL and Graph databases, as it can be answered via a combination of exact matching on record fields.

For reference, here's the correct answer to Task 2:

schwimmer	verein	zeit	ort	datum
Jochen Hanz	SG Neukölln Berlin	0:57,40	Hamburg-Dulsberg	2017-11-01
Jochen Hanz	SG Neukölln Berlin	0:58,43	Gelsenkirchen	2018-11-01
Peter Böhm	Marburger SV 1928	0:58,67	Hannover	2018-12-01
Peter Böhm	Marburger SV 1928	0:59,09	Bremen	2017-12-01
Matthias Michaelsen	SG Böhmetal	1:00,40	Bremen	2017-12-01
Michael Schmitz	SG Rhein-Erft-Köln	1:00,80	Bremen	2017-12-01
Dirk Neuhaus	SG Dortmund	1:01,71	Bremen	2017-12-01
Markus Bierig	SG Stadtwerke München	1:02,25	Eichstätt	2018-03-01
Paul Larsen	TSV Haar	1:03,59	Passau	2018-10-01
Kieran Garbutt	SV Bayreuth	1:03,75	Hannover	2018-12-01

Oh, look! Rank 9 has the same name as the blog post author.

Are our example tasks truly well defined?

As with all translations between business logic and computers, the costs of not being precise enough are real.

• The task formulation is still ambiguous. For example, is the desired answer separate top times lists for each year in question, or a single, aggregated list? My intention was a single-list as desired answer, but this requirement is at best implicit.

• The format of the desired response is also ambiguous. Is a list of times enough? Are the names of the swimmers also needed?

• For any swimmers out there, a further source of ambiguity is that the source data (recall: it's just a copy-paste from the DSV top-times tool) does not specify if the times are from a 25m or 50m pool. (It's from a 25m pool.)

Task 3 (relational and semantic) "What were the top 5 times in Germany for seasons 2017-18 and 2018-2019 for men in the 100m butterfly for the age group 40-44 for races featuring a good turn?"

This task combines both precise filter criteria involving dates (not to mention the geographical, age, gender, race-length and race type criteria) as well the semantic criterion about the turn being "good."

In showing the correct answer for Task 3, we give only the part of the race-description pertaining to a turn:

id	schwimmer	zeit	datum	turn-content
1	Jochen Hanz	0:57,40	2017-11-01	However, he made up for it with a great first turn, propelling himself forward with strong underwater dolphin kicks.
94	Jochen Hanz	0:58,43	2018-11-01	He had a great 1st turn as he approached the wall.
95	Peter Böhm	0:58,67	2018-12-01	He had a fast 2nd turn, propelling himself efficiently off the wall.
4	Michael Schmitz	1:00,80	2017-12-01	He had a fast second turn during the 100m butterfly race.
5	Dirk Neuhaus	1:01,71	2017-12-01	During the second turn, he executed a fast maneuver.

Overview of database technology for AI

There are whole books on subtopics of this topic, but at the risk of oversimplifying, let's break up the entire offering of databases for AI into three categories.

Relational databases for structured data. Relational databases have a data sweet spot made up of tables whose structure is largely static (e.g. the column names and data types don't change frequently) and whose entries can be linked together with some explicit join logic.

Examples include Postgresql, MySQL and SQLite. Though not strictly relational databases, for the purposes of this taxonomy and blog post, data warehouse offerings like BigQuery and Snowflake fit better among their relational cousins than with their NoSQL or vector database ones.

Not-only-SQL (NoSQL) databases for mixtures of structured and unstructured data. The data sweet spot for NoSQL databases consist of either structured data whose structure varies often (e.g. logs generated by applications or IoT data) or data that's primarily unstructured (text, audio, video) but with some tracking metadata attached to it (e.g. source url, timestamp when processed, media type).

Examples of NoSQL databases are MongoDB, Redis and DynamoDB.

Vector databases for unstructured data. The data sweet spot for vector databases is ... wait for it ... vectors! We'll discuss vectors and vector databases in greater detail below. As with NoSQL databases, they also typically store metadata associated with a vector.

Examples of vector databases are Chroma, Pinecone and Qdrant. As Andrej Karpathy has X'ed (though back then he tweeted it), the numerical python package NumPy shouldn't be overlooked when considering vector databases.

A few things that go missing while condensing all databases into a few paragraphs

• We have completely omitted graph databases and ad-hoc databases such as Excel.

• Saying vector databases are for unstructured data is an oversimplification in several ways. For example, images, audio and video are well suited to being stored in vector databases, yet each of these can be considered highly structured, as each of these is the product of rigid physical laws.

A very short introduction: the mathematics behind semantic similarity, vectors and vector databases

Perhaps you have a sense of what is meant by "semantic similarity," even if we haven't given a precise definition. If you are already familiar with this concept, then feel free to skip this section.

Informally, semantic similarity and search are for data questions where "you know what I mean?" is more appropriate than a precise enumeration of exact matching criteria.

What does semantic search have to do with vectors? Stepping back even further, what is a vector?

A vector is just a tuple (=list of fixed length) of numbers. When the length of the vector is small, we have many examples, as well as reliable intuition about their properties.

For example, latitude and longitude can be represented as a vector of length (or dimension) 2. The latitude and longitude of Ljubljana, Slovenia are approximately (46.1, 14.5). We know the world isn't a flat sheet, but is rather approximately a sphere in 3-d space, so we can also represent points on earth as tuples of three numbers.

Physics and history asides about a round Earth

Physical aside: the Earth is actually an ellipsoid, getting more and more smooshed along the poles every year due to the Earth's spinning motion.

Historical aside: contrary to popular accounts, the roundness of the Earth was discovered neither by Galileo nor Columbus (the latter claim is from a Washington Irving satirical story about the Spanish court and priesthood), but rather was accepted fact by nearly all medieval scholars in the West.

We thus get another example of vectors by considering locations on the Earth as points on a sphere in normal, three-dimensional space. This representation is better for calculating distances, and also will lead us directly to how even higher dimensional vectors can capture semantic similarity.

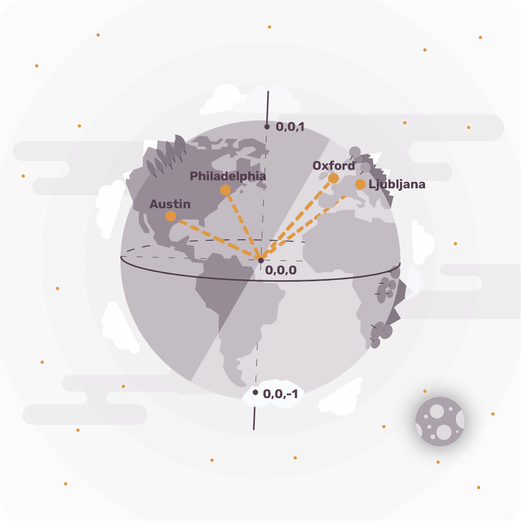
Considering locations on Earth as triples of numbers (x, y, z), with (0, 0, 0) being the center of the Earth, and (0, 0, 1) being the north pole, we have three-dimensional vectors. These tuples of 3 numbers for the cities Ljubljana, Slovenia, Oxford, UK, Philadelphia, PA, USA and Austin, TX, USA can be visualized as

and can be written mathematically as

• Ljubljana: (0.671888, 0.173839, 0.719963)

• Oxford: (0.618947, -0.013505, 0.785317)

• Philadelphia: (0.196289, -0.741017, 0.642156),

• Austin: (-0.116365, -0.855809, 0.504034)

There's a natural notion of similarity between locations on the Earth, too, as the inverse distance you have to travel "as the crow flies," or the Great Circle Distance.

Using this similarity score, we can calculate that

• cosine_similarity(ljubljana, oxford) = 0.98

• cosine_similarity(ljubljana, philadelphia) = 0.47

• cosine_similarity(ljubljana, austin) = 0.14

What's the furthest (or most dissimilar) you can get from Ljubljana? It's the place directly opposite Ljubljana through the center of the earth, which happens to be a spot in the Pacific Ocean off of New Zealand's Chatham Islands. For this spot, the similarity to Ljubljana is -1, meaning "opposite" of Ljubljana in a geographical sense.

Note that we've sneaked in the prefix cosine to our similarity measure. Mathematically, the similarity operation involves the trigonometric function cosine, but we won't go further under the hood here.

With natural language, and hence semantic search, the notion of similarity we want is not geographical, but meaning, something that is much harder to represent mathematically. Perhaps not surprisingly then, the vectors people use to capture meanings of words and sentences are not triples of numbers, but rather tuples of 384, 768 or other relatively long lists of numbers.

In these high dimensional spaces people use to represent language semantics, our physical intuitions of distance break down, so don't worry if you find spaces of more than 3 dimensions confusing---just think of them as lists of numbers and put physical intuition to the side. Historical and cultural aside: If you've come across the word "tesseract" either from the Avengers Infinity Stones or A Wrinkle in Time by Madeleine L'Engle, this four-dimensional object's name was coined by 19th century mathematician Charles Howard Hinton, who developed methods to visualize four dimensional space.

For example, if we want to find relevant text for the query turn_query = "Was there a good turn?", it should be the case that the similarity to description_good_turn = 'As he approached the first turn, he executed a smooth and quick flip' is higher than to description_bad_turn = 'He botched his 3rd turn, which cost him some time', which it is. Using the all-MiniLM-L6-v2 sentence encoder to transform text into vectors, we get that

• cosine_similarity(turn_query, description_good_turn) = 0.44

• cosine_similarity(turn_query, description_bad_turn) = 0.38

so that the question about a good turn is more similar to the description about a good flip turn than to the description of a bad turn.

What about race descriptions about the start, rather than turn? If our embedding is capturing the semantics we want to use for retrieval, then it should be the case that the similarity between the turn_query vector and the description_start='The swimmer was a bit slow off the blocks' is lower than between the turn_query and description_good_turn vectors, which, again, it is:

• cosine_similarity(turn_query, description_start) = 0.22

The unreasonable effectiveness of cosine similarity

This situation seems almost too good to be true. We take the whole domain of language meaning (at least in English), and reduce the question of semantic similarity to a simple mathematical operation that produces a single number: the closer to 1, the more similar, the closer to -1, the more different.

Cosine similarity is essentially a dumb approach. From a whole range of possible questions you can ask of data, with all of their nuances and imprecision, cosine similarity reduces the task of finding the "right" data to a single number: the distance between your question vector and potential answer vectors.

What's astounding is that this simple calculation is nevertheless so good at so many tasks. As we see in our example solutions below, the successes of vector embeddings and cosine similarity do not guarantee that your data retrieval problem is automagically solved. Even if vector similarity is the best approach, there are questions of which embedding model to use, not to mention text preprocessing and the relative importance of non-general domain vocabulary.

Vector databases

To round out the mathematics and algorithm parts, we spend just a few words on vector databases to give you an initial mental model and introduce some important names, but otherwise don't dive into technical detail.

Beyond the obvious function of efficiently storing vectors, the main feature of a vector database is its ability to perform efficient searching over the stored vectors. A main algorithm family for these searches is called "Approximate Nearest Neighbor (ANN)" search.

This peek into the mathematical of semantic similarity, vector embeddings and vector databases is just scratching the surface. My current favorite source for more details is Vicky Boyce's short book (or long article) What are Embeddings?.

Wrap-up

In this first part of two posts on databases for AI, we've articulated the renewed hope for robust semantic search thanks to GenAI advances, formulated some example data retrieval tasks that help us both test this hope in practice in Part 2, and presented background on language embeddings and databases.

The second post will look at how available technology succeeds and fails with these data retrieval tasks, make some predictions for the future of semantic search, and give advice for how to use the new tooling to solve your actual business problems.